组合-----剪枝优化

java

List<List<Integer>> res = new LinkedList<>();
    LinkedList<Integer> track = new LinkedList<>();
    public void backtracking(int n, int k, int startIndex) {
        if (track.size() == k) {
            res.add(new LinkedList<Integer>(track));
            return;
        }
        for (int i = startIndex; i <= n - (k - track.size()) + 1; i++) {
            track.add(i);
            backtracking(n, k, i + 1);
            track.removeLast();
        }
    }
    public List<List<Integer>> combine(int n, int k) {
        backtracking(n, k, 1);
        return res;
    }

go

var result [][]int
var track []int

func backtracking(n, k, startIndex int) {
	if len(track) == k {
		temp := make([]int, len(track))
		copy(temp, track)
		result = append(result, temp)
		return
	}
    for i := startIndex; i <= n - (k - len(track)) + 1; i++ {
		track = append(track, i)
		backtracking(n, k, i+1)
		track = track[:len(track)-1]
	}
}
func combine(n, k int) [][]int {
	result = make([][]int, 0)
    track = make([]int, 0, k)
	backtracking(n, k, 1)
	return result
}

c++

 vector<vector<int>> res;
    vector<int> track;
    void backtracking(int n, int k, int startIndex) {
        if (track.size() == k) {
            res.push_back(track);
            return;
        }
        for (int i = startIndex; i <= n - (k - track.size()) + 1; i++) {
            track.push_back(i);
            backtracking(n, k, i + 1);
            track.pop_back();
        }
    }
    vector<vector<int>> combine(int n, int k) {
        backtracking(n, k, 1);
        return res;
    }

分析

每一个结点需要进行选择，所以就对应一个完整的循环。

for (int i = startIndex; i <= n - (k - track.size()) + 1; i++) {
            track.add(i);
            backtracking(n, k, i + 1);
            track.removeLast();
        }

backtracking(n, k, i + 1); 是往下层继续寻找的过程。

简单总结一下，for 循环是横向，backtracking 是纵向搜索。

简单的分析一下循环的结束点，也就是至多从哪里开始搜。代码为什么这么写？

i <= n - (k - track.size()) + 1;

我们已经选择的元素个数为track.size()
所以我们还需要的元素的个数为k - track.size()
n 中剩余的元素为 [i, n]，所以剩余的元素个数也就是区间的大小为 n - i + 1
剩余元素的个数大于等于我们组合所需的个数，接下来就可以得到一个不等式 n - i + 1 >= k - track.size()
由上面的不等式可得i <= n - (k - track.size()) + 1

注：[i, n] 左右都是闭区间的元素的个数为 n - i + 1

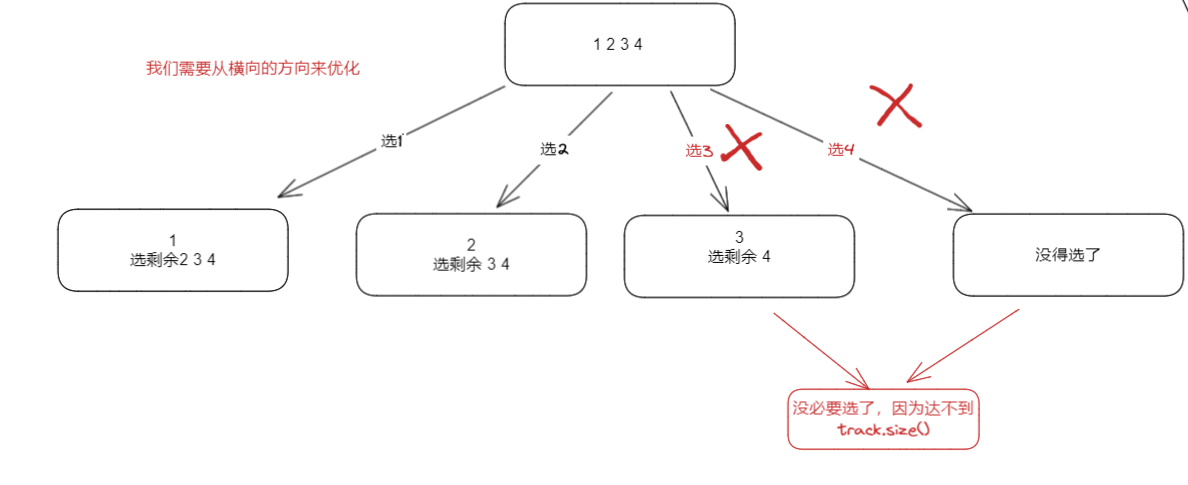
案例

我们可以通过一个简单的例子分析一下:


n = 4，k = 3
i  <= 4 - (3 - 0)) + 1
i < = 2